Question

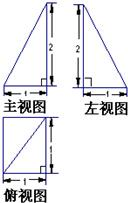
已知一个棱锥的三视图如图，单位：厘米．
（1）画出这个棱锥的直观图．
（2）求该棱锥的全面积．

Answer 1

分析：（1）由三视图可知该棱锥的直观图．（2）根据锥体的各面三角形的面积，可得棱锥的全面积．

解答：解：（1）三视图复原的几何体是底面为直角三角形，顶点在底面的射影是斜边的中点，（是正四棱锥的一部分）．如图：
（2）由直观图可知，其中锥体的高PO=4，底面等腰直角三角形的直角边AB=BC=6，所以AC=6

2

，侧面斜高为

42+32

=5．
所以侧面PAB和PBC的面积相同为，

1

2

×6×5=15，侧面PAC的面积为

1

2

×6

2

×4=12

2

，底面直角三角形ABC的面积为

1

2

×6×6=18，
所以该棱锥的全面积为2×15+18+12

2

=48+12

2

．

点评：本题主要考查三视图的识别和判断，以及空间几何体的表面积公式，考查学生的运算能力．