题目内容
复数
的共轭复数在复平面内对应的点位于（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
D
解析试题分析：根据除法运算可知，
,因此其共轭复数为
实部大于零，虚部小于零，故可知点在第四象限故选D
考点：复数的几何意义
点评：主要是考查了复数的运算以及复数的几何意义的运用，属于基础题。
练习册系列答案
阅读快车系列答案
相关题目
关于复数的命题：
（1）复数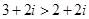
；（2）复数
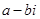的模为
；
（3）在复平面内,纯虚数与
轴上的点一一对应，其中真命题的个数是（ ）．
| A．0个 | B．1个 | C．2个 | D．3个 |
复数
= （ ）
A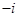． | B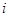． | C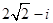． | D． |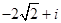
若复数
是实数，则
的值为
A． | B．3 |
| C．0 | D． |
设复数
，则复数
的虚部为（ ）
A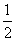． | B． | C． | D． |
复数
表示复平面内点位于( )
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
复数满足
，则复数
的实部与虚部之差为（ ）
A． | B． | C． | D． |
已知复数
满足
，则的实部 （ ）
A．不小于 | B．不大于 | C．大于 | D．小于 |
是虚数单位，则
的虚部是（ ）
A． | B． | C． | D． |