题目内容
设曲线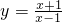 在点(3,2)处的切线的斜率为
在点(3,2)处的切线的斜率为
- A.2
- B.

- C.

- D.-2
C
分析:经过判断发现点(3,2)在曲线上,所以此点为切点,求出曲线方程的导函数,把切点的横坐标代入导函数中求出的函数值即为曲线方程的斜率.
解答:显然(3,2)在曲线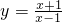 上,
上,
由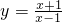 ,求出y′=
,求出y′= ,
,
把x=3代入得:y′|x=3=- ,即曲线方程的斜率为-
,即曲线方程的斜率为- .
.
故选C
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,是一道基础题.学生做题时注意判断已知点是否在曲线上,如果在的话此点即为切点.
分析:经过判断发现点(3,2)在曲线上,所以此点为切点,求出曲线方程的导函数,把切点的横坐标代入导函数中求出的函数值即为曲线方程的斜率.
解答:显然(3,2)在曲线
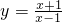 上,
上,由
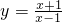 ,求出y′=
,求出y′= ,
,把x=3代入得:y′|x=3=-
 ,即曲线方程的斜率为-
,即曲线方程的斜率为- .
.故选C
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,是一道基础题.学生做题时注意判断已知点是否在曲线上,如果在的话此点即为切点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则a=( )
垂直,则a=( ) D.
D. 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
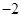 C.
C.
 D.
D.

 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
 C.
C.
 D.
D.

 在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )

 在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
在点(3,2)处的切线与直线ax+y+1=0垂直,则a=( )
