题目内容
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起,
使得△ABD与△ABC成直二面角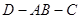 ,如图二,在二面角
,如图二,在二面角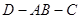 中.
中.
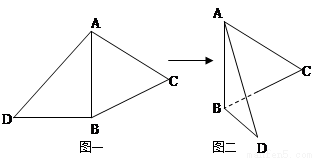
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
【答案】
(1)根据线面垂直的性质定理来得到线线垂直的证明。关键的一步是利用面ABD 面ABC,得到
面ABC,得到 BD
BD 面ABC,加以证明。
面ABC,加以证明。
(2) 2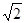 (3)
(3)
【解析】
试题分析: 解:(1)依题意,面ABD 面ABC,AB是交线,
面ABC,AB是交线,
而BD AB,
AB, BD
BD 面ABC,又AC
面ABC,又AC 面ABC,
面ABC,
 BD⊥AC;
4分
BD⊥AC;
4分
(2)由(1)知,BD面ABC,而BC 面ABC,
面ABC,
 BD⊥BC;Rt
BD⊥BC;Rt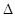 DBC中,BC=BA=2,BD=2,
DBC中,BC=BA=2,BD=2,
 DC=
DC=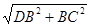 =
= =2
=2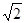 ;
8分
;
8分
(3)取AB的中点H,连CH、DH和DC,

 △ABC是正三角形,
△ABC是正三角形,
 CH
CH AB,又
AB,又 面ABC
面ABC 面ABD,
面ABD,
 CH
CH 面ABD,
面ABD,
 DH是DC在面ABD内的射影,
DH是DC在面ABD内的射影,

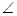 CDH是DC与面ABD成的角。
CDH是DC与面ABD成的角。
而CH=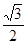 BC=
BC=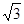 ,由(2)DC=2
,由(2)DC=2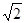 ,
,
 sin
sin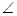 CDH=
CDH=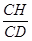 =
= =
= 即为所求。
12分
即为所求。
12分
考点:空间中点线面的位置关系
点评:解决该试题的关键是熟练的运用判定定理和性质定理得到垂直的证明,以及角的求解,属于基础题。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 选考题
选考题 如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是 ( )
如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则顶点C的轨迹是 ( ) 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分. (2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.
(2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.