题目内容
请阅读下列材料:对命题“若两个正实数a1,a2满足a12+a22=1,那么 .”
.”证明如下:构造函数f(x)=(x-a1)2+(x-a2)2,因为对一切实数x,恒有f(x)≥0,
又f(x)=2x2-2(a1+a2)x+1,从而得4(a1+a2)2-8≤0,所以
 .
.根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你可以构造函数g(x)= ,进一步能得到的结论为 .(不必证明)
【答案】分析:本题为有两个变量的关系问题归纳到n个变量的问题,构造的函数和得到的结论应与原式一致.
解答:解:由题意及归纳推理知识若n个正实数满足a12+a22+…+an2=1时,
可以构造函数g(x)=(x-a1)2+(x-a2)2+…(x-an)2
结论为:
故答案为:(x-a1)2+(x-a2)2+…(x-an)2; .
.
点评:本题考查归纳推理知识,属基本题型的考查.
解答:解:由题意及归纳推理知识若n个正实数满足a12+a22+…+an2=1时,
可以构造函数g(x)=(x-a1)2+(x-a2)2+…(x-an)2
结论为:

故答案为:(x-a1)2+(x-a2)2+…(x-an)2;
 .
.点评:本题考查归纳推理知识,属基本题型的考查.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
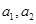 满足
满足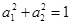 ,那么
,那么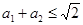 。”
。” ,因为对一切实数
,因为对一切实数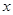 ,恒有
,恒有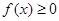 ,又
,又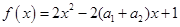 ,从而得
,从而得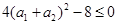 ,所以
,所以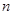 个正实数满足
个正实数满足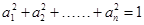 时,你可以构造函数
时,你可以构造函数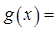 ,进一步能得到的结论为
。(不必证明)
,进一步能得到的结论为
。(不必证明)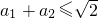 .”
.”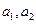 满足
满足 ,那么
,那么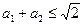 。”
。”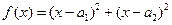 ,因为对一切实数
,因为对一切实数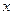 ,恒有
,恒有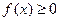 ,又
,又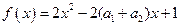 ,从而得
,从而得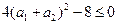 ,所以
,所以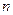 个正实数满足
个正实数满足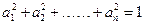 时,你可以构造函数
时,你可以构造函数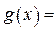 ,进一步能得到的结论为 。(不必证明)
,进一步能得到的结论为 。(不必证明)