题目内容
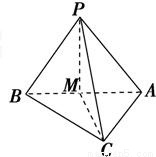
如图，已知△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、BD在平面ABC的同侧，M为EA的中点，CE=CA=2BD，
求证：（1）DE=DA；
（2）平面BDM⊥平面ECA．
求证：（1）DE=DA；
（2）平面BDM⊥平面ECA．
证明：（1）取AC中点N，连接MN、BN，∵△ABC是正三角形，∴BN⊥AC，
∵EC⊥平面ABC，BD⊥平面ABC，∴EC∥BD，EC⊥BN，
又∵M为AE中点，EC=2BD，∴MN
BD，∴BN
DM，
∴四边形MNBD是平行四边形，
由BN⊥AC，BN⊥EC，得BN⊥平面AEC，∴DM⊥平面AEC，
∴DM⊥AE，∴AD=DE．
（2）∵DM⊥平面AEC，DM?平面BDM，
∴平面BDM⊥平面AEC．
∵EC⊥平面ABC，BD⊥平面ABC，∴EC∥BD，EC⊥BN，
又∵M为AE中点，EC=2BD，∴MN
| ||
| . |
| ||
| . |
∴四边形MNBD是平行四边形，
由BN⊥AC，BN⊥EC，得BN⊥平面AEC，∴DM⊥平面AEC，
∴DM⊥AE，∴AD=DE．
（2）∵DM⊥平面AEC，DM?平面BDM，
∴平面BDM⊥平面AEC．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
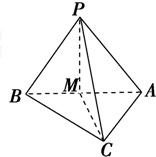10、如图，已知△ABC为直角三角形，其中∠ACB=90°，M为AB中点，PM垂直于△ABC所在平面，那么（ ）
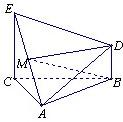如图，已知△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、BD在平面ABC的同侧，M为EA的中点，CE=CA=2BD，求证：
如图：已知△ABC为直角三角形，分别以直角边AC、BC为直径作半圆AmC和BnC，以AB为直径作半圆ACB，记两个月牙形阴影部分的面积之和为S1，△ABC的面积为S2，则S1与S2的大小关系为（ ）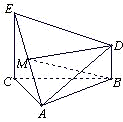
如图，已知△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、BD在平面ABC的同侧，M为EA的中点，CE=CA=2BD，