题目内容
等差数列{an}中a1>0,前n项和Sn,若S38=S12,则当Sn取得最大值时,n为
- A.26或27
- B.26
- C.25或26
- D.25
D
分析:设等差数列的公差为d,根据等差数列的前n项和的公式化简S4=S8,得到首项与公差的关系式,根据首项大于0得到公差d小于0,所以前n项和Sn是关于n的二次函数,由d小于0得到此二次函数为开口向下的抛物线,有最大值,则根据二次函数的对称性求出n的值,Sn取得最大值.
解答:由S38=S12,得:
38a1+ d=12a1+
d=12a1+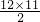 d,
d,
解得:a1=-637d,又a1>0,得到d<0,
所以Sn=na1+ d=
d= n2+(a1-
n2+(a1- )n,
)n,
由d<0,得到Sn是一个关于n的开口向下抛物线,且S38=S12,
由二次函数的对称性可知,当n= =25时,Sn取得最大值.
=25时,Sn取得最大值.
故选D.
点评:此题考查了等差数列的性质,考查了二次函数的图象与性质,是一道综合题.考查计算能力.
分析:设等差数列的公差为d,根据等差数列的前n项和的公式化简S4=S8,得到首项与公差的关系式,根据首项大于0得到公差d小于0,所以前n项和Sn是关于n的二次函数,由d小于0得到此二次函数为开口向下的抛物线,有最大值,则根据二次函数的对称性求出n的值,Sn取得最大值.
解答:由S38=S12,得:
38a1+
 d=12a1+
d=12a1+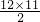 d,
d,解得:a1=-637d,又a1>0,得到d<0,
所以Sn=na1+
 d=
d= n2+(a1-
n2+(a1- )n,
)n,由d<0,得到Sn是一个关于n的开口向下抛物线,且S38=S12,
由二次函数的对称性可知,当n=
 =25时,Sn取得最大值.
=25时,Sn取得最大值.故选D.
点评:此题考查了等差数列的性质,考查了二次函数的图象与性质,是一道综合题.考查计算能力.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目