题目内容
5.已知函数$f(x)=\left\{{\begin{array}{l}{{2^x},x≤0}\\{{{log}_2}x,x>0}\end{array}}\right.$(1)在所给的平面直角坐标系中画出函数f(x)的图象;
(2)利用图象求f(x)=$\frac{1}{2}$时x的值;
(3)当0<f(x)<$\frac{1}{2}$时,求x的取值范围.
分析 (1)分段作出函数图象;
(2)观察图象得出x的值;
(3)分x≤0和x>0两种情况讨论解出x.
解答 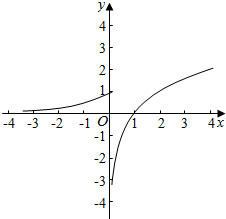 解:(1)f(x)的图象如图所示:
解:(1)f(x)的图象如图所示:
(2)①若x≤0,则2x=$\frac{1}{2}$,解得x=-1;
②若x>0,则log2x=$\frac{1}{2}$,解得x=$\sqrt{2}$.
综上,当f(x)=$\frac{1}{2}$时x=-1或x=$\sqrt{2}$.
(3)①若x≤0,则0<2x$<\frac{1}{2}$,解得x<-1,
②若x>0,则0<log2x$<\frac{1}{2}$,解得1$<x<\sqrt{2}$.
综上,当$0<f(x)<\frac{1}{2}$时,x的取值范围是(-∞,-1)∪(1,$\sqrt{2}$).
点评 本题考查了分段函数的图象和性质,常涉及分类讨论思想,属于基础题.

练习册系列答案
相关题目
16.在等比数列{an}中,a1=-3,a2=-6,则a4的值为( )
| A. | -24 | B. | 24 | C. | ±24 | D. | -12 |
10.已知集合A={y|y=log2x,0<x<1},B={y|y=($\frac{1}{2}$)x,x>1},则(∁RA)∩B=( )
| A. | (0,$\frac{1}{2}$) | B. | (0,1) | C. | ($\frac{1}{2}$,1) | D. | ∅ |
14.已知a>b>0,椭圆C1的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,双曲线C2的方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,C1与C2的离心率之积为$\frac{{\sqrt{3}}}{2}$,则双曲线C2的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.