题目内容
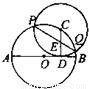
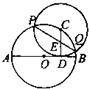
如图,已知AB为⊙O的弦,CD切⊙O于P,AC⊥CD于C,BD⊥DC于D,PQ⊥AB于Q.
求证:PQ2=AC·BD.
答案:
解析:
解析:
|
证明:连结PA、PB,如图,
因为CD切⊙O于P, 所以∠1=∠2. 因为AC⊥CD于C,PQ⊥AB于Q, 所以∠ACP=∠PQB=90°. 所以△ACP∽△PQB. 所以AC∶PQ=AP∶PB. 同理,△BDP∽△PQA,所以PQ∶BD=AP∶PB. 所以AC∶PQ=PQ∶BD, 即PQ2=AC·BD. 分析:欲证PQ2=AC·BD,只需证AC∶PQ=PQ∶BD,图中没有产生比例中项的条件,需要通过过渡比来解决.连结PA、PB,如图,利用弦切角定理,得到不相邻的两对直角三角形分别相似. |

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

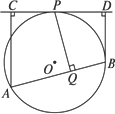
 11、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是
11、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是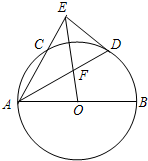 (2012•武昌区模拟)(几何证明)如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
(2012•武昌区模拟)(几何证明)如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若 (2011•太原模拟)如图,已知AB为半圆O的直径,BE、CD分别为半圆的切线,切点分别为B、C,DC的延长线交BE于F,AC的延长线交BE于E.AD⊥DC,D为垂足.
(2011•太原模拟)如图,已知AB为半圆O的直径,BE、CD分别为半圆的切线,切点分别为B、C,DC的延长线交BE于F,AC的延长线交BE于E.AD⊥DC,D为垂足.