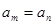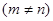题目内容
有下面四个判断:
①命题“设a、b∈R,若a+b≠6,则a≠3或b≠3”是一个假命题;
②若“p或q”为真命题,则p、q均为真命题;
③命题“∀a、b∈R,a2+b2≥2(a﹣b﹣1)”的否定是“∃a、b∈R,a2+b2≤2(a﹣b﹣1)”;
④若函数![]() 的图象关于原点对称,则a=﹣1.其中正确的有 (只填序号)
的图象关于原点对称,则a=﹣1.其中正确的有 (只填序号)
④
| 解答: | 解:①当a=3且b=3时,a+b=6,所以命题正确,根据逆否命题和原命题的等价性可知,若a+b≠6,则a≠3或b≠3”为真命题,∴①错误. ②若“p或q”为真命题,则p、q至少有一个为真命题,∴②错误. ③根据全称命题的否定是特称命题,∴命题“∀a、b∈R,a2+b2≥2(a﹣b﹣1)”的否定是“∃a、b∈R,a2+b2<2(a﹣b﹣1)”,∴③错误. ④若函数 故答案为:④. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
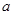 、
、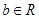 ,若
,若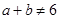 ,则
,则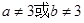 ”是一个假命题
”是一个假命题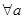 、
、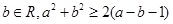 ”的否定是:
”的否定是: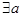 、
、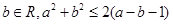 ”
”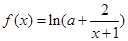 的图象关于原点对称,则
的图象关于原点对称,则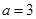
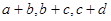 也成等比数列;
也成等比数列;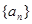 既是等差数列,也是等比数列,则
既是等差数列,也是等比数列,则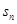 ,且
,且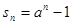 ,(a
,(a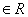 ),则
),则