题目内容
三棱锥P-ABC中,PA,PB,PC两两互相垂直,且PA=1,PB=PC=
,则点P到平面ABC的距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
分析:先根据三棱锥P-ABC中,PA、PB、PC两两互相垂直可构造一个以PA、PB、PC为长宽高的长方体,点P到平面ABC的距离视为点P到平面ABC的距离,利用三棱锥P-ABC的体积=三棱锥C-ABP的体积即可求得点P到平面ABC的距离.
解答: 解:∵三棱锥P-ABC中,PA、PB、PC两两互相垂直
解:∵三棱锥P-ABC中,PA、PB、PC两两互相垂直
∴构造一个以PA、PB、PC为长宽高的长方体(如图)
三棱锥P-ABC的体积=
S △ABC×d(d为点P到平面ABC的距离)
三棱锥C-ABP的体积=
S △ABP×PC,
∵三棱锥P-ABC的体积=三棱锥C-ABP的体积,
∴
S △ABC×d=
S △ABP×PC,
则d=
,
则点P到平面ABC的距离为
故选:A
 解:∵三棱锥P-ABC中,PA、PB、PC两两互相垂直
解:∵三棱锥P-ABC中,PA、PB、PC两两互相垂直∴构造一个以PA、PB、PC为长宽高的长方体(如图)
三棱锥P-ABC的体积=
| 1 |
| 3 |
三棱锥C-ABP的体积=
| 1 |
| 3 |
∵三棱锥P-ABC的体积=三棱锥C-ABP的体积,
∴
| 1 |
| 3 |
| 1 |
| 3 |
则d=
| ||
| 2 |
则点P到平面ABC的距离为
| ||
| 2 |
故选:A
点评:本题主要考查了点线面的距离的计算,以及构造法的运用等有关知识,同时考查了空间想象能力,计算能力,以及转化与划归的思想,属于基础题.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.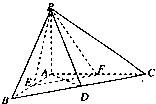 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,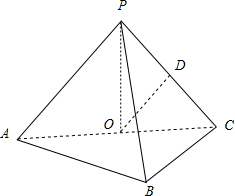 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.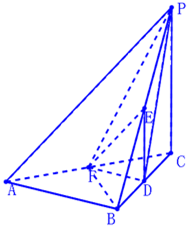 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.