题目内容
15.在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立坐标系.已知点A的极坐标为($\sqrt{2}$,$\frac{π}{4}$),直线L的直角坐标方程为x+y=a,且点A在直线上L.(1)求a的值;
(2)圆C的参数方程为$\left\{{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}}$,(α为参数),试判断直线L与圆C的位置关系并说明理由.
分析 (1)利用点的坐标在极坐标曲线时,直接求解a即可.
(2)求出圆的圆的与半径,通过点到直线的距离与半径比较,得到结果即可.
解答 解:(1)由点$A(\sqrt{2},\frac{π}{4})$在直线$ρcos(θ-\frac{π}{4})=a$上,可得a=2
所以直线的方程可化为ρcosθ+ρsinθ=2
从而直线的直角坐标方程为x+y-2=0
(2)由已知得圆C的直角坐标方程为(x-1)2+y2=1
所以圆心为(1,0),半径r=1
以为圆心到直线的距离$d=\frac{{\sqrt{2}}}{2}<1$,所以直线与圆相交.
点评 本题考查极坐标与参数方程的应用,点到直线的距离以及直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3.设p:f(x)=ex+lnx+$\frac{1}{2}$x2+mx+2在(0,+∞)内单调递增,q:m≥-4,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.某几何体的三视图如图所示,则该几何体的体积为( )
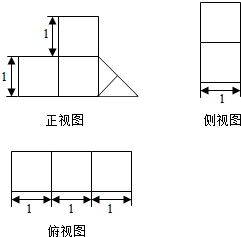

| A. | $\frac{7}{3}$ | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
7.设i是虚数单位,复数$\frac{{-2\sqrt{3}+i}}{{1+2\sqrt{3}i}}$=( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
 如图,正方体ABC-A1B1C1D1中,点F为A1D的中点.
如图,正方体ABC-A1B1C1D1中,点F为A1D的中点.