题目内容
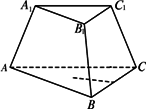
如图，正三棱台ABC－A1B1C1中，已知AB＝10，棱台一个侧面梯形的面积为
，O1、O分别为上、下底面正三角形中心，D1D为棱台的斜高，∠D1DA＝60°.求上底面的边长．
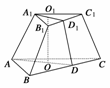
由AB＝10，
则AD＝
AB＝5
，
OD＝
AD＝
.
设上底面边长为x，则O1D1＝
x.
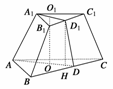过D1作D1H⊥AD于H，
则DH＝OD－OH＝OD－O1D1＝－x，
在△D1DH中，D1D＝
＝2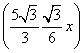
，
∴在梯形B1C1CB中，S＝
(B1C1＋BC)·D1D，
∴＝(x＋10)·2，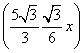
∴40＝(x＋10)(10－x)．∴x＝2
，
∴上底面的边长为2.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
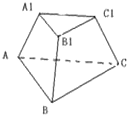如图所示，在正三棱台ABC-A1B1C1中，上、下底面的边长分别为3cm和6cm，高为
