题目内容
已知函数f(x)=Asin2(ωx+φ)(A>0,ω>0,0<φ< ),且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
),且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(Ⅰ)求?;
(Ⅱ)计算f(1)+f(2)+…+f(2008).
解:(I)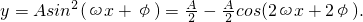
∵y=f(x)的最大值为2,A>0.
∴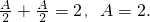
又∵其图象相邻两对称轴间的距离为2,ω>0,
∴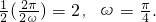
∴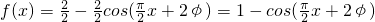 .
.
∵y=f(x)过(1,2)点,∴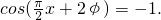
∴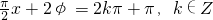 ,∴
,∴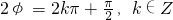 ,
,
∴ ,
,
又∵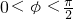 ,
,
∴ .
.
(II)解法一:∵ ,BC⊥B1C
,BC⊥B1C
∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又∵y=f(x)的周期为4,2008=4×502,
∴f(1)+f(2)++f(2008)=4×502=2008.
解法二:∵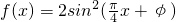
∴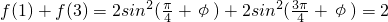 ,
,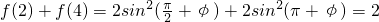 ,
,
∴f(1)+f(2)+f(3)+f(4)=4.
又(±2,0)的周期为4,2008=4×502,
∴f(1)+f(2)++f(2008)=4×502=2008.
分析:(Ⅰ)根据最值求出A,其图象相邻两对称轴间的距离为2,求出周期,确定ω,过点(1,2)求?;
(Ⅱ)法一:根据函数的正确化简f(1)+f(2)+…+f(2008).然后求出它的值即可.
法二:利用三角函数的平方关系,求出一个周期内的f(1)+f(3),f(2)+f(4)的值,然后求出表达式的值.
点评:本题考查三角函数的最值,三角函数的周期性及其求法,y=Asin(ωx+φ)中参数的物理意义,通过题目条件,正确求出函数的表达式,挖掘条件,利用周期正确解答是解好三角函数题目的关键,本题考查计算能力,是基础题.
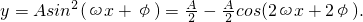
∵y=f(x)的最大值为2,A>0.
∴
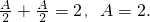
又∵其图象相邻两对称轴间的距离为2,ω>0,
∴
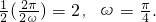
∴
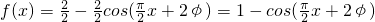 .
.∵y=f(x)过(1,2)点,∴
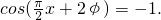
∴
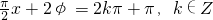 ,∴
,∴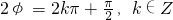 ,
,∴
 ,
,又∵
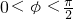 ,
,∴
 .
.(II)解法一:∵
 ,BC⊥B1C
,BC⊥B1C∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又∵y=f(x)的周期为4,2008=4×502,
∴f(1)+f(2)++f(2008)=4×502=2008.
解法二:∵
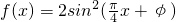
∴
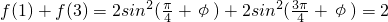 ,
,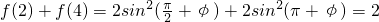 ,
,∴f(1)+f(2)+f(3)+f(4)=4.
又(±2,0)的周期为4,2008=4×502,
∴f(1)+f(2)++f(2008)=4×502=2008.
分析:(Ⅰ)根据最值求出A,其图象相邻两对称轴间的距离为2,求出周期,确定ω,过点(1,2)求?;
(Ⅱ)法一:根据函数的正确化简f(1)+f(2)+…+f(2008).然后求出它的值即可.
法二:利用三角函数的平方关系,求出一个周期内的f(1)+f(3),f(2)+f(4)的值,然后求出表达式的值.
点评:本题考查三角函数的最值,三角函数的周期性及其求法,y=Asin(ωx+φ)中参数的物理意义,通过题目条件,正确求出函数的表达式,挖掘条件,利用周期正确解答是解好三角函数题目的关键,本题考查计算能力,是基础题.

练习册系列答案
相关题目