题目内容
如果函数f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0,试求a、b、c的值.
解:y′=5ax4-3bx2.令y′=0,即5ax4-3bx2=0,x2(5ax2-3b)=0.
∵x=±1是极值点,∴5a(±1)2-3b=0.又x2=0,
∴可疑点为x=0,x=±1.若a>0,y′=5ax2(x2-1),当x变化时,y′、y的变化情况如下表:
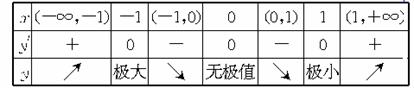
由上表可知,当x=-1时,f(x)有极大值,当x=1时,f(x)有极小值.
∴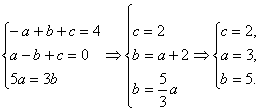
若a<0,同理可得a=-3,b=-5,c=2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
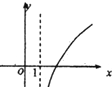
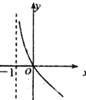

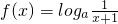 的图象大致是
的图象大致是



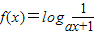 的图象大致是( )
的图象大致是( )



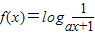 的图象大致是( )
的图象大致是( )



 的图象大致是( )
的图象大致是( )