Question

（本小题满分12分）

在如图所示的几何体中，四边形ABCD为平行四边形，∠ ACB=，ＥＡ⊥平面ＡＢＣＤ，EF∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ.

（Ⅰ）若Ｍ是线段ＡＤ的中点，求证：ＧＭ∥平面ＡＢＦＥ;

（Ⅱ）若ＡＣ＝ＢＣ=２ＡＥ,求二面角Ａ-ＢＦ-Ｃ的大小．

Answer 1

（I）证法一：

因为EF//AB，FG//BC，EG//AC，，

所以∽

由于AB=2EF，

因此，BC=2FC，

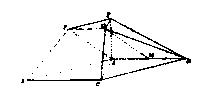连接AF，由于FG//BC，

在中，M是线段AD的中点，

则AM//BC，且

因此FG//AM且FG=AM，

所以四边形AFGM为平行四边形，

因此GM//FA。

又平面ABFE，平面ABFE，

所以GM//平面AB。

证法二：

因为EF//AB，FG//BC，EG//AC，，

所以∽

由于AB=2EF，

因此，BC=2FC，

取BC的中点N，连接GN，

因此四边形BNGF为平行四边形，

所以GN//FB，

在中，M是线段AD的中点，连接MN，

则MN//AB，

因为

所以平面GMN//平面ABFE。

又平面GMN，

所以GM//平面ABFE。

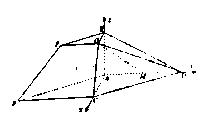
   （II）解法一：

因为，

又平面ABCD，

所以AC，AD，AE两两垂直，

分别以AC，AD，AE所在直线为x轴、y轴和z轴，建立如图所法的空间直角坐标系，

不妨设

则由题意得A（0，0，0，），B（2，-2，0），C（2，0，0，），E（0，0，1），

所以

又

所以

设平面BFC的法向量为

则

所以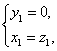取

所以

设平面ABF的法向量为，

则

所以

则，

所以

因此二面角A—BF—C的大小为

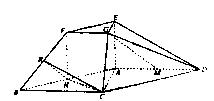解法二：

由题意知，平面平面ABCD，

取AB的中点H，连接CH，

因为AC=BC，

所以，

则平面ABFE，

过H向BF引垂线交BF于R，连接CR，

则

所以为二面角A—BF—C的平面角。

由题意，不妨设AC=BC=2AE=2。

在直角梯形ABFE中，连接FH，

则，又

所以

因此在中，

由于

所以在中，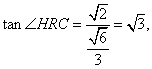

因此二面角A—BF—C的大小为