题目内容
给出定义:若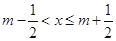 (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数 最近的整数,记作
最近的整数,记作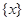 ,即
,即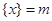 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数 的四个命题:
的四个命题:
①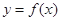 的定义域是
的定义域是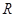 ,值域是
,值域是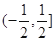 ;②点
;②点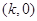 是
是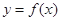 的图像的对称中心,其中
的图像的对称中心,其中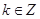 ;③函数
;③函数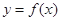 的最小正周期为1;④函数
的最小正周期为1;④函数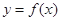 在
在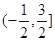 上是增函数.则上述命题中真命题的序号是( )
上是增函数.则上述命题中真命题的序号是( )
| A.①④ | B.①③ | C.②③ | D.②④ |
B
解析试题分析::由题意知, ,则得到
,则得到 ,则命题①为真命题;由于
,则命题①为真命题;由于 时,
时, ,但由于
,但由于 ,故函数不是中心对称图形,故命题②为假命题;由题意知,函数
,故函数不是中心对称图形,故命题②为假命题;由题意知,函数 ,故它的最小正周期为1,则命题③为真命题;由于,
,故它的最小正周期为1,则命题③为真命题;由于, ,则得到f(x)=x-{x}为分段函数,且在
,则得到f(x)=x-{x}为分段函数,且在 ,
, 为增函数,但在区间
为增函数,但在区间 上不是增函数,故命题④为假命题.正确的命题为①③,故答案为①③.
上不是增函数,故命题④为假命题.正确的命题为①③,故答案为①③.
考点:命题的真假判断与应用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
给出下列四个命题:
①命题p: ∈R,sinx≤1,则
∈R,sinx≤1,则 :
: ∈R,sinx<1.
∈R,sinx<1.
②当a≥1时,不等式|x-4|+|x-3|<a的解集为非空.
③当x>0时,有lnx+ ≥2.
≥2.
④设复数z满足(1-i)z=2i,则z=1-i.
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设 是平面
是平面 内两条不同的直线,是平面
内两条不同的直线,是平面 外的一条直线,则
外的一条直线,则 是
是 的( )
的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
如果命题“ ”为假命题,则( )
”为假命题,则( )
A. 均为假命题 均为假命题 | B. 均为真命题 均为真命题 |
C. 中至少一个为真命题 中至少一个为真命题 | D. 中至多有一个为真命题 中至多有一个为真命题 |
若 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“存在 ,使
,使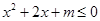 ”的否定是( )
”的否定是( )
A.存在 ,使 ,使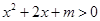 |
B.不存在 ,使 ,使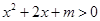 |
C.对于任意 ,都有 ,都有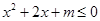 |
D.对于任意 ,都有 ,都有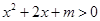 |
有下列四个命题:
①函数 的值域是
的值域是 ;
;
②平面内的动点P到点 和到直线
和到直线 的距离相等,则P的轨迹是抛物线;
的距离相等,则P的轨迹是抛物线;
③直线 与平面
与平面 相交于点B,且
相交于点B,且 与
与 内相交于点C的三条互不重合的直线
内相交于点C的三条互不重合的直线 所成的角相等,则
所成的角相等,则 ;
;
④若 ,则
,则
其中正确的命题的编号是( )
| A.①③ | B.②④ | C.②③ | D.③④ |
已知 且
且 ,则“
,则“ ”是 “
”是 “ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“ ,
, ”的否定是( )
”的否定是( )
A. , , | B. , , |
C. , , | D. , , |