题目内容
已知函数f(x)=(1-a2)x2-2bx+b2(-1<b-1<a).用card(A)表示集合A中元素的个数,若使得f(x)>0成立的充分必要条件是x∈A,且card(A∩Z)=4,则实数a的取值范围是
- A.(-1,2)
- B.(1,2)
- C.(2,3)
- D.(3,4)
B
分析:由card(A∩Z)=4知A中恰有4个整数,
即不等式f(x)>0的解集中恰有4个整数解,
再由f(x)>0?(x-b)2-(ax)2>0?[(1-a)x-b][(1+a)x-b]>0求解.
分类讨论,当-1<a≤1时,原不等式的解集不符合题意;a>1求出 的解集即可.
的解集即可.
解答:依题意A中恰有4个整数,所以不等式f(x)>0的解集中恰有4个整数解.
因为f(x)>0?(x-b)2-(ax)2>0?[(1-a)x-b][(1+a)x-b]>0,
当-1<a≤1时,原不等式的解集不符合题意;
当a>1时,[(1-a)x-b][(1+a)x-b]>0?(a-1)(a+1)[x-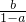 ][x-
][x- ]<0,
]<0,
所以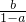 <x<
<x< .
.
因为 ∈(0,1),所以
∈(0,1),所以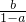 ∈(-4,-3).所以3a-3<b<4a-4.
∈(-4,-3).所以3a-3<b<4a-4.
又0<b<1+a,所以 解得1<a<2.
解得1<a<2.
故选B.
点评:本题主要考查集合的关系和不等式的解法,在解题中1-a和1+a处在系数位置要注意正负的讨论.
分析:由card(A∩Z)=4知A中恰有4个整数,
即不等式f(x)>0的解集中恰有4个整数解,
再由f(x)>0?(x-b)2-(ax)2>0?[(1-a)x-b][(1+a)x-b]>0求解.
分类讨论,当-1<a≤1时,原不等式的解集不符合题意;a>1求出
 的解集即可.
的解集即可.解答:依题意A中恰有4个整数,所以不等式f(x)>0的解集中恰有4个整数解.
因为f(x)>0?(x-b)2-(ax)2>0?[(1-a)x-b][(1+a)x-b]>0,
当-1<a≤1时,原不等式的解集不符合题意;
当a>1时,[(1-a)x-b][(1+a)x-b]>0?(a-1)(a+1)[x-
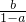 ][x-
][x- ]<0,
]<0,所以
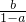 <x<
<x< .
.因为
 ∈(0,1),所以
∈(0,1),所以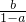 ∈(-4,-3).所以3a-3<b<4a-4.
∈(-4,-3).所以3a-3<b<4a-4.又0<b<1+a,所以
 解得1<a<2.
解得1<a<2.故选B.
点评:本题主要考查集合的关系和不等式的解法,在解题中1-a和1+a处在系数位置要注意正负的讨论.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|