题目内容
(本小题满分12分)设数列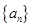 和
和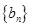 满足:
满足: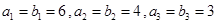 ,数列
,数列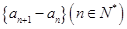 是等差数列,
是等差数列, 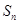 为数列
为数列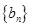 的前
的前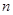 项和,且
项和,且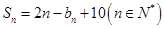 ,
,
(I)求数列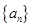 和
和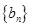 的通项公式;
的通项公式;
(II)是否存在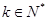 ,使
,使 ?若存在,求出
?若存在,求出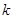 ,若不存在,说明理由。
,若不存在,说明理由。
【答案】
(I) ,
,
(II)不存在 ,使
,使
【解析】(I)由已知





当 时,也满足上式,
时,也满足上式, 

由

 ,即
,即 ,则
,则 ,
,
∴数列 是等比数列,公比
是等比数列,公比 ,
,


(II)设
当 时:
时: 是
是 的增函数;
的增函数; 也是
也是 的增函数。
的增函数。
 时:
时: ,又
,又
 不存在
不存在 ,使
,使


练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目