题目内容
圆拱桥的水面跨度为24米,拱高为8米,现有一船,船宽为10米,载货后货物宽度与船的宽度相同,如果这条船想从桥下通过,则该船水面以上最高不能超过
米.
| 119 |
| 18 |
| 119 |
| 18 |
分析:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0),将B(12,-8)代入,求得抛物线方程,求出A的纵坐标,即可求得结论.
解答: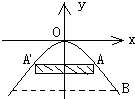 解:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0)
解:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0)
将B(12,-8)代入得p=9,∴x2=-18y,
当船两侧与抛物线接触时不能通过,
设点A(5,yA),由52=-18yA,得yA=-
,
所以h=8-
=
米
故答案为:
 解:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0)
解:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0)将B(12,-8)代入得p=9,∴x2=-18y,
当船两侧与抛物线接触时不能通过,
设点A(5,yA),由52=-18yA,得yA=-
| 25 |
| 18 |
所以h=8-
| 25 |
| 18 |
| 119 |
| 18 |
故答案为:
| 119 |
| 18 |
点评:本题考查抛物线的应用,是中档题.解题时要认真审题,恰当地建立坐标系,合理地进行等价转化.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目