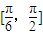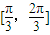题目内容
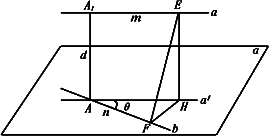
已知两条异面直线a,b所成的角为![]() ,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n.求证:EF=
,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n.求证:EF=![]()
答案:
解析:
解析:
|
解:过A作 ∵AA1⊥a,∴A1A⊥ ∴AA1⊥b, ∴A1A垂直 ∵a∥ ∵a∥ ∴A1A=EH=d,AH=A1E=m ∵A1A⊥α ∴EH⊥α. ∵FH 在RtΔFHE中,EF= ∵ 即∠HAF= 由余弦定理得 FH2=m2+n2-2mncos ∴EF= 当F(或E)在A(或A1)的另一侧时,同理可得 EF= 综上所述,EF= |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知两条异面直线a,b所成的角为
,直线l与a,直线l与b所成的角为θ,则θ的范围是( )
| π |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
 β=c,则
β=c,则 β=c,则
β=c,则
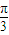 ,直线l与a,直线l与b所成的角为θ,则θ的范围是( )
,直线l与a,直线l与b所成的角为θ,则θ的范围是( )