题目内容
过点M(0,4)、被圆 截得的线段长为
截得的线段长为 的直线方程为 .
的直线方程为 .
【答案】
x=0或15x+8y-32=0;
【解析】
试题分析:当直线与x轴垂直时,圆心到直线的距离为:1,半径位,则弦长为:2 ,符合题意;
,符合题意;
当直线与x轴不垂直时设直线的斜率为k,则直线方程为y-4=kx,
圆心到直线的距离为 ,根据勾股定理可知4-
,根据勾股定理可知4- =3,求得k=-
=3,求得k=- ,
,
∴直线方程为15x+8y-32=0
故所求直线的方程为:x=0或15x+8y-32=0。
考点:本题主要考查直线与圆的位置关系、直线方程。
点评:研究直线与圆的位置关系,可根据条件灵活选用“代数法”或“几何法”。圆的半弦长、半径、弦心距构成Rt△,在解“弦问题”中常常用到。本题易漏斜率不存在的情况。

练习册系列答案
相关题目
 的直线方程为 .
的直线方程为 .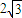 的直线方程为 .
的直线方程为 .