题目内容
已知函数
，
.
图象恒过定点
，
且点既在
图象上，又在
的导函数的图象上.
（Ⅰ）求
的值；
（Ⅱ）设
，求证：当
且
时，
；
（Ⅲ）求证：
（
且
）.
（Ⅰ）因为
所以
恒过
所以
所以
因为
所以
即，.
（Ⅱ）证：
，即证
时，
异号
因为
所以当
时，
因为
所以在
单调递减，又
所以
所以
因为当
时，
所以
所以
所以
综上得证.
（Ⅲ）因为
令
（）
所以
所以
……
所以
所以
.
练习册系列答案
高效智能课时作业系列答案
相关题目
且
的图象恒过定点
，则
. 
且
的图象恒过定点
，则
(x∈R) 图象恒过点(2,0)，则a2＋b2的最小值为 ( )
C．4 D.
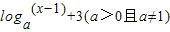的图象恒过点P，若角α的终边经过点P，则cos2α-sin2α的值等于 ．
反函数的图象恒过定点
，则点
上，若
则
的最小值为 ．