题目内容
已知函数f(x)=| 3 |
（1）求函数f（x）的最大值和最小值；
（2）设函数f（x）在[-1，1]上的图象与x轴的交点从左到右分别为M、N，图象的最高点为P，求
| PM |
| PN |
分析：（1）利用两角和差的正弦公式 化简函数的解析式为f（x）=2sin(πx+
)，根据-1≤sin(πx+
)≤1，
求得函数f（x）的最大值和最小值．
（2）令f(x)=2sin(πx+
)=0，求出M、N两点的坐标，由sin(πx+
)=1，求出点P的坐标，
由 cos＜
，
＞=
求得结果．
| π |
| 6 |
| π |
| 6 |
求得函数f（x）的最大值和最小值．
（2）令f(x)=2sin(πx+
| π |
| 6 |
| π |
| 6 |
由 cos＜
| PM |
| PN |
| ||||
|
|
解答：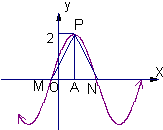
解：（1）∵f(x)=
sinπx+cosπx=2(
sinπx+
cosπx)
=2sin(πx+
)．
∵x∈R，∴-1≤sin(πx+
)≤1，
∴函数f（x）的最大值和最小值分别为2，-2．
（2）令f(x)=2sin(πx+
)=0，得πx+
=kπ，k∈Z，
∵x∈[-1，1]，∴x=-
，或x=
，∴M(-
，0)，N(
，0)，
由sin(πx+
)=1，且x∈[-1，1]得 x=
，∴P(
，2)，
∴
=(-
，-2)，
=(
，-2)，从而 cos＜
，
＞=
=
．
解：（1）∵f(x)=| 3 |
| ||
| 2 |
| 1 |
| 2 |
=2sin(πx+
| π |
| 6 |
∵x∈R，∴-1≤sin(πx+
| π |
| 6 |
∴函数f（x）的最大值和最小值分别为2，-2．
（2）令f(x)=2sin(πx+
| π |
| 6 |
| π |
| 6 |
∵x∈[-1，1]，∴x=-
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| 6 |
| 5 |
| 6 |
由sin(πx+
| π |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
∴
| PM |
| 1 |
| 2 |
| PN |
| 1 |
| 2 |
| PM |
| PN |
| ||||
|
|
| 15 |
| 17 |
点评：本题考查两角和差的正弦公式，三角函数的最值，两个向量夹角公式的应用，求出M、N两点的坐标，是解题的难点．
练习册系列答案
相关题目