题目内容
(本小题满分13分)已知函数 ,数列
,数列 满足
满足

(1)若数列 是常数列,求t的值;
是常数列,求t的值;
(2)当 时,记
时,记 ,证明:数列
,证明:数列 是等比数列,并求出通项公式an.
是等比数列,并求出通项公式an.
 ,数列
,数列 满足
满足
(1)若数列
 是常数列,求t的值;
是常数列,求t的值;(2)当
 时,记
时,记 ,证明:数列
,证明:数列 是等比数列,并求出通项公式an.
是等比数列,并求出通项公式an.解 (Ⅰ)∵数列 是常数列,∴
是常数列,∴ ,即
,即 ,解得
,解得 ,
,
或 .
.
∴所求实数 的值是1或-1. …………………………5分
的值是1或-1. …………………………5分
(Ⅱ) ,
, ,
,
即 . ……9分
. ……9分
∴数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是
 .……11分
.……11分
由 ,即
,即 ,解得
,解得 .
.
∴所求的通项公式 .………… 13分
.………… 13分
 是常数列,∴
是常数列,∴ ,即
,即 ,解得
,解得 ,
,或
 .
.∴所求实数
 的值是1或-1. …………………………5分
的值是1或-1. …………………………5分(Ⅱ)
 ,
, ,
,即
 . ……9分
. ……9分∴数列
 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是 .……11分
.……11分由
 ,即
,即 ,解得
,解得 .
.∴所求的通项公式
 .………… 13分
.………… 13分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
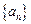 中,
中,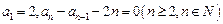 .
.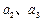 的值(只写结果)并求出数列
的值(只写结果)并求出数列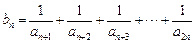 ,求
,求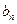 的最大值
的最大值 满足
满足 且
且 ,则
,则 等于( )
等于( )







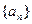 的前
的前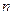 项和
项和 满足
满足
 的值; (2)求
的值; (2)求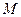 使下列不等式:
使下列不等式: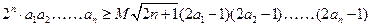
 成立?若存在,求出M的取值范围;若不存在,请说明理由
成立?若存在,求出M的取值范围;若不存在,请说明理由 ,则
,则 ( )
( )



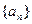 为等差数列, {bn}为等比数列, 且a1=b1=1,a2+a4=b3, b2b4=a3,分别求出{an}与{bn}的通项公式.
为等差数列, {bn}为等比数列, 且a1=b1=1,a2+a4=b3, b2b4=a3,分别求出{an}与{bn}的通项公式.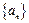 的各项均是正数,其前
的各项均是正数,其前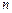 项和为
项和为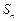 ,满足
,满足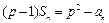 ,其中
,其中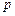 为正常数,且
为正常数,且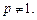
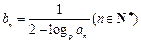 ,数列
,数列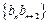 的前
的前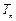 ,求证:
,求证: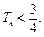
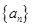 满足
满足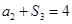 ,
,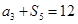 ,则
,则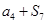 的值是( )
的值是( )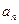 }的前
}的前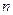 项和
项和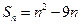 ,若它的第
,若它的第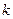 项满足
项满足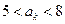 ,则
,则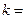 .
.