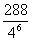题目内容
 从足够多的四种颜色的灯泡中任选六个安置在如图的6个顶点处,则相邻顶点处灯泡颜色不同的概率为
从足够多的四种颜色的灯泡中任选六个安置在如图的6个顶点处,则相邻顶点处灯泡颜色不同的概率为
- A.

- B.

- C.

- D.

C
分析:本题是一个等可能事件的概率,试验发生包含的事件是从四种颜色的灯泡中选出一个放在一个顶点处,有4种选法,6个顶点共有46种结果,满足条件的事件是若用三种颜色和用四种颜色两种不同的情况,做出所有的事件数,得到概率.
解答:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是从四种颜色的灯泡中选出一个放在一个顶点处,有4种选法,
6个顶点共有46种结果,
满足条件的事件是若用三种颜色:先选颜色有4种可能,然后放下底面 3×2×1=6种,
放好后,放上底面有2×1×1=2种
共有4×6×2=48种;
用四种颜色时,下底面4×3×2=24种,
放好后,第四种颜色有3种,另两个位置有1×1+1×2=3种,
共有24×3×3=216种
所有方法为48+216=264种
∴满足条件的概率是
故选C.
点评:本题考查等可能事件的概率和计数原理的应用,本题解题的关键是做出满足条件的事件数,注意此处的分类的应用.
分析:本题是一个等可能事件的概率,试验发生包含的事件是从四种颜色的灯泡中选出一个放在一个顶点处,有4种选法,6个顶点共有46种结果,满足条件的事件是若用三种颜色和用四种颜色两种不同的情况,做出所有的事件数,得到概率.
解答:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是从四种颜色的灯泡中选出一个放在一个顶点处,有4种选法,
6个顶点共有46种结果,
满足条件的事件是若用三种颜色:先选颜色有4种可能,然后放下底面 3×2×1=6种,
放好后,放上底面有2×1×1=2种
共有4×6×2=48种;
用四种颜色时,下底面4×3×2=24种,
放好后,第四种颜色有3种,另两个位置有1×1+1×2=3种,
共有24×3×3=216种
所有方法为48+216=264种
∴满足条件的概率是

故选C.
点评:本题考查等可能事件的概率和计数原理的应用,本题解题的关键是做出满足条件的事件数,注意此处的分类的应用.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 从足够多的四种颜色的灯泡中任选六个安置在如图的6个顶点处,则相邻顶点处灯泡颜色不同的概率为( )
从足够多的四种颜色的灯泡中任选六个安置在如图的6个顶点处,则相邻顶点处灯泡颜色不同的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
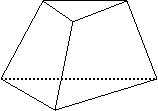 A.
A.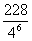 B.
B.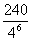 C.
C.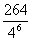 D.
D.