题目内容

已知三次函数f（x）=ax³-x²+x在（0，+∞）存在极大值点，则a的范围是

A.
$数学公式$
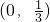
B.
$数学公式$
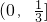
C.
$数学公式$
D.
$数学公式$

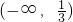
D
分析：先求出f′（x）=3ax²-2x+1，由题意得到f′（x）=0有两个不同的正实数根或一正一负根，列出等价条件△＞0且a≠0，再进行求解．
解答：由题意知，f′（x）=3ax²-2x+1，
∵三次函数f（x）=ax³-x²+x在（0，+∞）存在极大值点，
∴f′（x）=3ax²-2x+1=0有两个不同的正实数根或一正一负根，
①当a＞0时，此时3ax²-2x+1=0有两个不同的正实数根，
∴ $\text{[math]}$ ，即0＜a＜ $\text{[math]}$ ，
②当a＜0时，此时3ax²-2x+1=0有一正一负根，
只须△＞0，即4-12a＞0，?a $\text{[math]}$ ，
∴a＜0
综上，则a的范围是 $\text{[math]}$
故选D．
点评：本题考查了导数与函数的单调性的关系，本题的易错点是容易忽略二次项的系数不为零．

练习册系列答案

经纶学典中考档案系列答案

优倍伴学总复习系列答案

中考对策全程复习方案系列答案

王朝霞中考真题精编系列答案

阅读旗舰文言文课内阅读系列答案

中考一线题系列答案

中考真题超详解系列答案

中考必刷题系列答案

新课程新练习系列答案

53随堂测系列答案

相关题目

已知三次函数f（x）=ax³+bx²+cx（a，b，c∈R）．
（Ⅰ）若函数f（x）过点（-1，2）且在点（1，f（1））处的切线方程为y+2=0，求函数f（x）的解析式；
（Ⅱ）在（Ⅰ）的条件下，若对于区间[-3，2]上任意两个自变量的值x₁，x₂都有|f（x₁）-f（x₂）|≤t，求实数t的最小值；
（Ⅲ）当-1≤x≤1时，|f′（x）|≤1，试求a的最大值，并求a取得最大值时f（x）的表达式．

19、已知三次函数f（x）=x³+ax²+bx+c在x=1和x=-1时取极值，且f（-2）=-4．
（I）求函数y=f（x）的表达式；
（II）求函数y=f（x）的单调区间和极值；
（Ⅲ）若函数g（x）=f（x-m）+4m（m＞0）在区间[m-3，n]上的值域为[-4，16]，试求m、n应满足的条件．

已知三次函数f（x）=ax³+bx²+cx+d，（a，b，c，d∈R），命题p：y=f（x）是R上的单调函数；命题q：y=f（x）的图象与x轴恰有一个交点．则p是q的（　　）

A．充分但不必要条件

B．必要但不充分条件

C．充要条件

D．既不充分也不必要条件

已知三次函数f（x）=x³+ax²+bx+c在x=1和x=-1时取极值，且f（-2）=-4．
（1）求函数f（x）的表达式；
（2）求函数的单调区间和极值；
（3）求函数在区间[-2，5]的最值．

已知三次函数f（x）=ax³+bx²+cx+d的图象如图所示，则