题目内容
设z是复数,试解方程z•
-3i
=1+3i.
| . |
| z |
| . |
| z |
设z=x+yi,其中x,y∈R,…(2分)
则
= x - yi,原方程可以化成:
(x+yi)(x-yi)-3i(x-yi)=1+3i,即 x2+y2-3xi-3y=1+3i,
即 (x2+y2-3y)-3xi=1+3i.…(6分)
故有
,…(8分)
解得
,或
,…(10分)
故z1=-1,z2=-1+3i.…(12分)
则
| . |
| z |
(x+yi)(x-yi)-3i(x-yi)=1+3i,即 x2+y2-3xi-3y=1+3i,
即 (x2+y2-3y)-3xi=1+3i.…(6分)
故有
|
解得
|
|
故z1=-1,z2=-1+3i.…(12分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
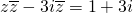 .
. .
.