题目内容
已知椭圆
+
=1(a>b>0),c=
,圆(x-c)2+y2=c2与椭圆恰有两个公共点,则椭圆的离心率e的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
分析:由题意,算出圆(x-c)2+y=c2的圆心为椭圆的右焦点且半径r=c.再根据圆与椭圆有两个公共点,得到椭圆的右顶点在圆的内部,由此建立关于a、c的不等式,解之可得椭圆的离心率.
解答:解:∵椭圆
+
=1中,c=
,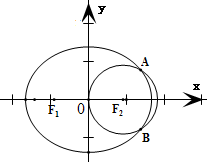
∴椭圆的焦点为F1(-c,0)和F2(c,0).
由此可得圆(x-c)2+y=c2的圆心为F2(c,0),半径r=c.
∵圆(x-c)2+y=c2与椭圆恰有两个公共点,
∴椭圆的右顶点(a,0)在圆的内部,
可得(a-c)2+02=c2,解之得a<2c,
因此椭圆的离心率e=
>
,结合e∈(0,1),可得
<e<1.
故答案为:
<e<1
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |

∴椭圆的焦点为F1(-c,0)和F2(c,0).
由此可得圆(x-c)2+y=c2的圆心为F2(c,0),半径r=c.
∵圆(x-c)2+y=c2与椭圆恰有两个公共点,
∴椭圆的右顶点(a,0)在圆的内部,
可得(a-c)2+02=c2,解之得a<2c,
因此椭圆的离心率e=
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题给出以椭圆的右焦点为圆心且半径等于半焦距的圆,在该圆与椭圆有两个公共点的情况下,求椭圆的离心的范围.着重考查了椭圆的标准方程与简单几何性质、点与圆的位置关系等知识,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目