题目内容
在圆x2+y2=4上，与直线4x+3y-12=0的距离最小的点的坐标是（ ）A．（
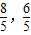）B．（
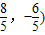
C．（-
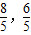）D．
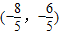
【答案】分析：在圆x2+y2=4上，与直线4x+3y-12=0的距离最小的点，必在过圆心与直线4x+3y-12=0垂直的直线上，求此线与圆的交点，根据图象可以判断坐标．
解答：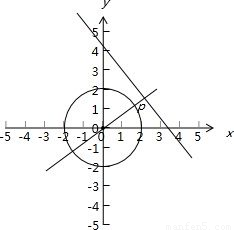
解：圆的圆心（0，0），过圆心与直线4x+3y-12=0垂直的直线方程：3x-4y=0，
它与x2+y2=4的交点坐标是（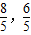
），
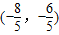
又圆与直线4x+3y-12=0的距离最小，
所以所求的点的坐标（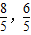
）．图中P点为所求；
故选A．
点评：本题考查点到直线的距离公式，直线与圆的位置关系，直线的截距等知识，是中档题．
解答：
解：圆的圆心（0，0），过圆心与直线4x+3y-12=0垂直的直线方程：3x-4y=0，它与x2+y2=4的交点坐标是（
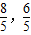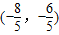
），又圆与直线4x+3y-12=0的距离最小，
所以所求的点的坐标（
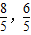）．图中P点为所求；故选A．
点评：本题考查点到直线的距离公式，直线与圆的位置关系，直线的截距等知识，是中档题．
练习册系列答案
相关题目
在圆x2+y2=4上，与直线4x+3y-12=0的距离最小的点的坐标是（ ）
A、（
| ||||
B、（
| ||||
C、（-
| ||||
D、(-
|
如图所示，点N在圆x2+y2=4上运动，DN⊥x轴，点M在DN的延长线上，且