题目内容
已知定义在实数集R上的函数 满足
满足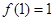 ,且
,且 的导数
的导数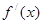 在R上恒有
在R上恒有 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. | C. | D.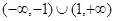 |
D
解析试题分析:因为 ,所以
,所以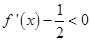 ,即
,即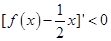 ,故
,故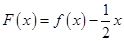 为
为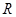 上的减函数,而
上的减函数,而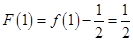 ,所以原不等式化为
,所以原不等式化为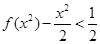 ,即
,即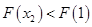 ,利用单调性有
,利用单调性有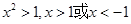 ,故原不等式的解集为
,故原不等式的解集为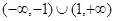 ,选D.
,选D.
考点:利用导数研究函数单调性、抽象函数、一元二次不等式的解法.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
以初速度40m/s竖直向上抛一物体,t秒时刻的速度v=40-10t2,则此物体达到最高时的高度为( ).
A.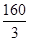 m m | B.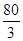 m m | C.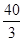 m m | D.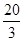 m m |
若曲线 在点
在点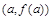 处的切线与两条坐标轴围成的三角形的面积为18,则
处的切线与两条坐标轴围成的三角形的面积为18,则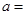 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
若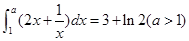 ,则
,则 的值是( )
的值是( )
| A.2 | B.3 | C.4 | D.6 |
已知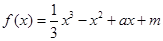 ,其中
,其中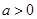 ,如果存在实数
,如果存在实数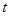 ,使
,使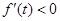 ,则
,则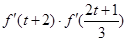 的值为( )
的值为( )
| A.必为正数 | B.必为负数 | C.必为非负 | D.必为非正 |
若函数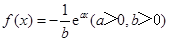 的图象在
的图象在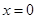 处的切线与圆
处的切线与圆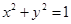 相切,则
相切,则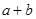 的最大值是( )
的最大值是( )
| A.4 | B.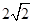 | C.2 | D.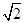 |
如果函数 满足:对于任意的
满足:对于任意的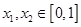 ,都有
,都有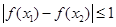 恒成立,则
恒成立,则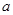 的取值范围是( )
的取值范围是( )
A.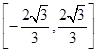 | B. |
C.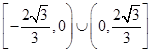 | D.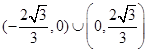 |
若函数 在
在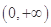 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A.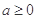 | B.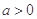 | C.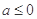 | D.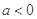 |
设 是定义在R上的奇函数,且
是定义在R上的奇函数,且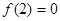 ,当
,当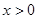 时,有
时,有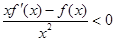 恒成立,则不等式
恒成立,则不等式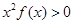 的解集是( )
的解集是( )
| A.(-2,0) ∪(2,+∞) | B.(-2,0) ∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |