Question

【题目】已知椭圆的左、右焦点分别为F1，F2，过点F1的直线与C交于A，B两点.△ABF2的周长为，且椭圆的离心率为.

（1）求椭圆C的标准方程：

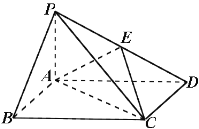
（2）设点P为椭圆C的下顶点，直线PA，PB与y＝2分别交于点M，N，当|MN|最小时，求直线AB的方程.

Answer 1

【答案】（1）（2）x﹣y+1＝0

【解析】

（1）根据三角形的周长求得，结合椭圆离心率和求得的值，由此求得椭圆的标准方程.

（2）设出直线的方程，联立直线的方程和椭圆的方程，写出韦达定理.通过直线的方程求得，通过直线的方程求得，由此求得的表达式并进行化简，对进行分类讨论，由此求得的最小值以及此时直线的方程.

（1）由题意可得：4a＝，，

∴a，c＝1，∴b2＝a2﹣c2＝1，

∴椭圆C的方程为：；

（2）点P（0，﹣1），F1（﹣1，0），设A（x1，y1），B（x2，y2），

显然直线AB与x轴不重合，设直线AB的方程为：x＝my﹣1，则可知m≠﹣1，

联立方程，消去y得：（m2+2）y2﹣2my﹣1＝0，

∴，，

直线PA的方程为：（y1+1）x﹣x1y﹣x1＝0，可得，

同理，

|MN|＝||＝3||＝3，

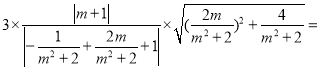
当m＝0时，|MN|＝6，

当m≠0时，|MN|＝，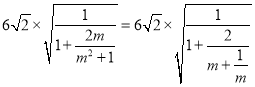

由于m∈（﹣∞，﹣2）∪[2，+∞），则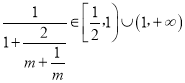，此时|MN|的最小值为6＜，在m＝1处取得，

综上所述，当|MN|最小时，直线AB的方程为：x＝y﹣1，即x﹣y+1＝0.