题目内容
已知![]() 、
、![]() 都是定义在R上的函数,若存在实数m、n使得
都是定义在R上的函数,若存在实数m、n使得![]() ,则称
,则称![]() 为
为![]() 、
、![]() 在R上生成的函数。若
在R上生成的函数。若![]() ,
,![]() .
.
(1)判断函数![]() 是否为
是否为![]() 、
、![]() 在R上生成的函数,并说明理由;
在R上生成的函数,并说明理由;
(2)记![]() 为
为![]() 、
、![]() 在R上生成的一个函数,若
在R上生成的一个函数,若![]() ,且
,且![]() 的最大值为4,
的最大值为4,
求![]() 。
。
解:(1)函数![]() 不是
不是![]() 、
、![]() 在R上生成的函数。
在R上生成的函数。
理由:假设函数![]() 是
是![]() 、
、![]() 在R上生成的函数,
在R上生成的函数,
则存在实数m、n使得![]()
令![]() ,得
,得![]() ①
①
令![]() ,得
,得![]() ②
②
由①②矛盾知:函数![]() 不是
不是![]() 、
、![]() 在R上生成的函数
在R上生成的函数
(2)设![]()
![]()
则![]() , ∴
, ∴ ![]() , ∴
, ∴ ![]()
设![]() ,则函数
,则函数![]() 可化为:
可化为:![]() ,
,![]()
当![]() 时,函数化为:
时,函数化为:![]() ,
,![]()
∵ 当![]() 时,
时,![]() ∴
∴ ![]() ,符合题意
,符合题意
当![]() 时,函数化为:
时,函数化为:![]()
当![]() 时,即
时,即![]() 时
时
∵ 当![]() 时,
时,![]()
∴ 由![]() 得
得![]() ,不符合
,不符合![]() 舍去
舍去
当![]() 时,即
时,即![]() 或
或![]() (舍去)时
(舍去)时
∵ 当![]() 时,
时,![]()
∴ 由![]() ,得
,得![]() 或
或![]() (舍去)
(舍去)
∴ ![]() ∴
∴ ![]() ,符合题意
,符合题意
当![]() 时,即
时,即![]() 时,不符合
时,不符合![]() 舍去
舍去
当![]() 时,函数
时,函数![]() 的对称轴
的对称轴![]()
∵ 当![]() 时,
时,![]()
∴ 由![]() 得
得![]() ,不符合
,不符合![]() 舍去
舍去
综上所述,![]() 或
或![]()

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目








 、
、 都是定义在R上的函数,
都是定义在R上的函数, ,
, ,
, ,
, ,则关于
,则关于 的方程
的方程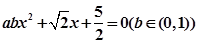 有两个不同实根的概率为( )
有两个不同实根的概率为( ) B.
B. C.
C. D.
D.
 ,
, 都是定义在R上的函数,
都是定义在R上的函数, ,
, ,
,
 ,且
,且 ,
, ,在有穷数列
,在有穷数列

 中,任意取正整数
中,任意取正整数 ,则前
,则前 项和大于
项和大于 的概率是
的概率是  ,
, 都是定义在R上的函数,
都是定义在R上的函数, ,且
,且

 =
= .现任取正整数
.现任取正整数 ,则在有穷数列{
,则在有穷数列{ }(n=1,2,¼,10)中前k项和大于
}(n=1,2,¼,10)中前k项和大于 的概率是( )
的概率是( ) B.
B. C.
C. D.
D.