题目内容
(10分)已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x0∈R,x+2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
【答案】
a≤-2或a=1
【解析】
试题分析:由“p且q”是真命题,则p为真命题,q也为真命题.
若p为真命题,a≤x2恒成立,
∵x∈[1,2],∴a≤1. …………………5分
若q为真命题,即x2+2ax+2-a=0有实根,
Δ=4a2-4(2-a)≥0,即a≥1或a≤-2,………………10分
综上,实数a的取值范围为a≤-2或a=1. …………………12分
考点:特称命题全称命题的真假
点评:p且q为真命题需满足命题p为真命题,命题q为真命题

练习册系列答案
相关题目
 在R上是减函数;命题q:在平面直角坐标系中,点
在R上是减函数;命题q:在平面直角坐标系中,点 在直线
在直线 的左下方。若
的左下方。若 为假,
为假, 为真,求实数
为真,求实数 的取值范围
的取值范围 ,命题q:
,命题q: ,若
,若 与
与 都为假命题,求x的值。
都为假命题,求x的值。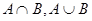 ;
;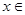 ∁U(A∪B), 命题q:
∁U(A∪B), 命题q: 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ;
; ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.