题目内容
在数列{an} 中，a1=1，a n+1=3an+（n+1）•3n（n∈N*），
（Ⅰ）设bn=
，求数列{bn} 的通项公式；
（Ⅱ）求数列{
}的前n项和Sn．
解：（Ⅰ）a n+1=3an+（n+1）•3n，两边同除3n+1，
∴
，
即bn+1=bn+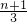
，
所以bn=（bn-bn-1）+（bn-1-bn-2）+…+（ b2-b1）+b1，又b1=
=
，
故
．
（Ⅱ）由（Ⅰ）可知bn=，得
，所以
=
，
…①
…②
①-②得：
，
所以
．
分析：（Ⅰ）通过a n+1=3an+（n+1）•3n，两边同除3n+1，得到数列{}，利用累加法求数列{bn} 的通项公式；
（Ⅱ）结合（Ⅰ）求出数列{an} 的通项公式，得到数列{}的通项公式，利用错位相减法直接求数列{}的前n项和Sn．
点评：本题是中档题考查数列通项公式的应用，数列前n项和的求法，考查计算能力，转化思想．
∴
，即bn+1=bn+
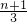，所以bn=（bn-bn-1）+（bn-1-bn-2）+…+（ b2-b1）+b1，又b1=
=，故
．（Ⅱ）由（Ⅰ）可知bn=
，得，所以=，…①…②①-②得：
，所以
．分析：（Ⅰ）通过a n+1=3an+（n+1）•3n，两边同除3n+1，得到数列{
}，利用累加法求数列{bn} 的通项公式；（Ⅱ）结合（Ⅰ）求出数列{an} 的通项公式，得到数列{
}的通项公式，利用错位相减法直接求数列{}的前n项和Sn．点评：本题是中档题考查数列通项公式的应用，数列前n项和的求法，考查计算能力，转化思想．
练习册系列答案
名校课堂系列答案
相关题目