题目内容
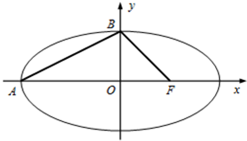 如图所示,在椭圆
如图所示,在椭圆| x2 |
| a2 |
| y2 |
| b2 |
(I)若△ABF为等腰三角形,且BF=2,求椭圆方程;
(II)若△ABF为钝角三角形,求椭圆离心率的取值范围.
分析:(I)先由题意可知AB=
>a,AF=a+c>a,BF=a,因为△ABF为等腰三角形,得到
=a+c从而解得c=
-1最后根据a,b,c 的关系求得a,b的值,写出椭圆方程;(
(II)由题意可知,∠ABF为钝角,由余弦定理可知,(
)2+a2-(a+c)2<0转化为:e2+e-1>0,解之即可得到椭圆离心率取值范围.
| a2+b2 |
| a2+b2 |
| 3 |
(II)由题意可知,∠ABF为钝角,由余弦定理可知,(
| a2+b2 |
解答:解:(I)由题意可知AB=
>a,AF=a+c>a,BF=a,
因为△ABF为等腰三角形,所以AB=AF,即
=a+c.(3分)
两边平方,得a2+b2=(a+c)2,整理得a2-2ac-2c2=0
因为a=BF=2,解得c=
-1,(6分)b2=a2-c2=2
,
所以椭圆方程为
+
=1.(8分)
(II)若△ABF为钝角三角形,由题意可知,∠ABF为钝角,(10分)
由余弦定理可知,(
)2+a2-(a+c)2<0,(12分)
整理得,a2-ac-c2<0,即e2+e-1>0,
解得e>
或e<
,(14分)
又因为0<e<1,所以椭圆离心率取值范围是
<e<1.(16分)
| a2+b2 |
因为△ABF为等腰三角形,所以AB=AF,即
| a2+b2 |
两边平方,得a2+b2=(a+c)2,整理得a2-2ac-2c2=0
因为a=BF=2,解得c=
| 3 |
| 3 |
所以椭圆方程为
| x2 |
| 4 |
| y2 | ||
2
|
(II)若△ABF为钝角三角形,由题意可知,∠ABF为钝角,(10分)
由余弦定理可知,(
| a2+b2 |
整理得,a2-ac-c2<0,即e2+e-1>0,
解得e>
-1+
| ||
| 2 |
-1-
| ||
| 2 |
又因为0<e<1,所以椭圆离心率取值范围是
-1+
| ||
| 2 |
点评:本题主要考查了椭圆的简单性质.解题的关键是通过挖掘题设信息找到a和c的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 设b>0,椭圆方程为
设b>0,椭圆方程为 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且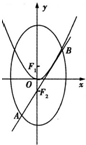 如图所示,椭圆C:
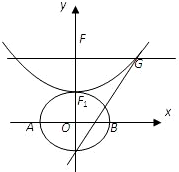
如图所示,椭圆C: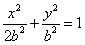 ,抛物线方程为x2=8(y-b),如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
,抛物线方程为x2=8(y-b),如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,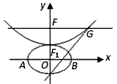
 设b>0,椭圆方程为
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.