Question

设S_n是等差数列｛a_n｝前n项的和，已知S₃与S₄的等比中项为S₅，S₃与S₄的等差中项为1，求等差数列｛a_n｝的通项a_n.

Answer 1

设等差数列｛a_n｝的首项为a，公差为d，则a_n=a+(n-1)d,?

前n项和为 S_n=na+,?

 

由题意得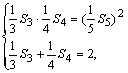其中S₅≠0.?

 

于是得?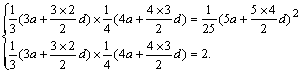

 

整理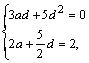得解得?

 

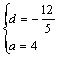由此得a_n=1;或a_n=4-(n-1)=-n.

 

经验证a_n=1时，S₅=5，或a_n=-n时，?S₅=-4，均适合题意.

 

故所求数列通项公式为a_n=1,或a_n=-n.