题目内容
中心在原点,焦点在x轴上的椭圆C的焦距为2,两准线间的距离为10.设A(5,0),B(1,0).(1)求椭圆C的方程;
(2)过点A作直线与椭圆C只有一个公共点D,求过B,D两点,且以AD为切线的圆的方程;(6分)
(3)过点A作直线l交椭圆C于P,Q两点,过点P作x轴的垂线交椭圆C于另一点S,若![]() =t
=t![]() (t>1),求证:
(t>1),求证:![]() =t
=t![]() .
.
解:(1)设椭圆的标准方程为![]() +
+![]() =1(a>b>0),依题意得
=1(a>b>0),依题意得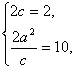 得
得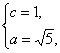 ∴b2=4.
∴b2=4.
∴椭圆的标准方程为![]() +
+![]() =1.
=1.
(2)设过点A的直线方程为y=k(x-5),代入椭圆方程![]() +
+![]() =1得
=1得
(4+5k2)x2-50k2x+125k2-20=0.(*)依题意得Δ=0,即(50k2)2-4(4+5k2)(125k2-20)=0,
得k=±![]() ,且方程的根为x=1,∴D(1,±
,且方程的根为x=1,∴D(1,±![]() ).
).
当点D位于x轴上方时,过点D与AD垂直的直线与x轴交于点E,
直线DE的方程是y-![]() =
=![]() (x-1),∴E(
(x-1),∴E(![]() ,0).
,0).
所求圆即为以线段DE为直径的圆,故方程为(x![]() )2+(y
)2+(y![]() )=
)=![]() .
.
同理可得:当点D位于x轴下方时,圆的方程为(x![]() )2+(y+
)2+(y+![]() )=
)=![]() .
.
(3)设P(x1,y1),Q(x2,y2),由![]() =t
=t![]() 得
得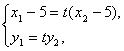 代入
代入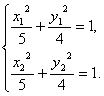
∴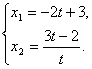 (**)要证
(**)要证![]() =t
=t![]() ,即证
,即证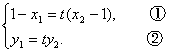
由方程组(**)可知方程组①成立,②显然成立.∴![]() =t
=t![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
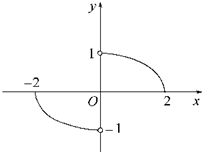 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
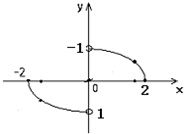 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
 .
.