题目内容
如图,平面 平面
平面 ,四边形
,四边形 为矩形,
为矩形, .
. 为
为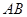 的中点,
的中点, .(1)求证:
.(1)求证: ;(2)若
;(2)若 与平面
与平面 所成的角为
所成的角为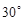 ,求二面角
,求二面角 的余弦值.
的余弦值.
(1)证明见解析;(2)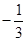 .
.
解析试题分析:(1)本小题证明的是线线垂直,把问题转化为证明线面垂直(线面垂直 线线垂直),即证
线线垂直),即证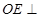 平面
平面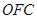 ,从而有
,从而有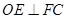 ;(2)本小题可从传统几何方法及空间向量方法入手,法一:先证
;(2)本小题可从传统几何方法及空间向量方法入手,法一:先证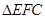 ,
,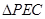 为等边三角形,取
为等边三角形,取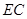 的中点
的中点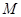 ,连结
,连结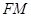 ,
,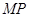 ,可证得
,可证得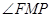 为二面角
为二面角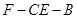 的平面角,在三角形FMP中用余弦定理的推论完成求值;法二:利用空间向量解决面面角问题,只需找到这两个面的法向量
的平面角,在三角形FMP中用余弦定理的推论完成求值;法二:利用空间向量解决面面角问题,只需找到这两个面的法向量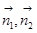 ,利用公式
,利用公式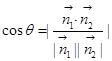 完成计算即可,但要注意本题面面角为钝二面角.
完成计算即可,但要注意本题面面角为钝二面角.
试题解析:(1)证明:连结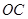 ,因
,因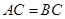 ,
, 是
是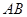 的中点,故
的中点,故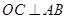 .又因平面
.又因平面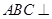 平面
平面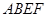 ,故
,故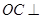 平面
平面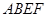 ,于是
,于是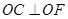 .又
.又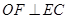 ,所以
,所以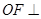 平面
平面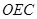 ,所以
,所以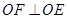 ,又因
,又因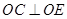 ,故
,故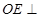 平面
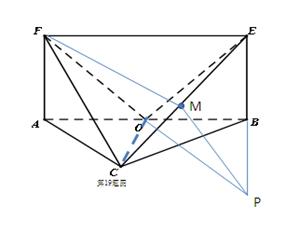
平面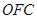 ,所以
,所以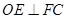 .
.
(2)解法一:由(1),得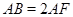 .不妨设
.不妨设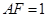 ,
,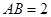 .因
.因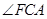 为直线
为直线 与平面
与平面 所成的角,故
所成的角,故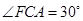 ,所以
,所以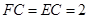 ,
,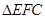 为等边三角形.设
为等边三角形.设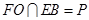 ,则
,则 ,
,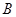 分别为
分别为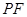 ,
,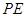 的中点,
的中点,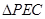 也是等边三角形.取
也是等边三角形.取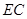 的中点
的中点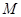 ,连结
,连结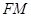 ,
,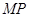 ,则
,则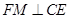 ,
,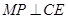 ,所以
,所以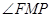 为二面角
为二面角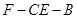 的平面角.在
的平面角.在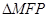 中,
中,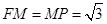 ,
,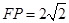 ,故
,故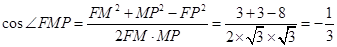 ,即二面角
,即二面角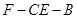 的余弦值为
的余弦值为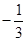 .
.
解法二:取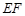 的中点
的中点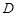 ,以
,以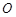 为原点,
为原点,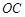 ,
,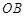 ,
,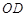 所在的直
所在的直

练习册系列答案
相关题目
 中,
中, 于
于 ,三边分别是
,三边分别是 ,则有
,则有 ;类比上述结论,写出下列条件下的结论:四面体
;类比上述结论,写出下列条件下的结论:四面体 中,
中, 的面积分别是
的面积分别是 ,二面角
,二面角 的度数分别是
的度数分别是 ,则
,则 .
. 中,
中, 丄平面
丄平面 ,
, 丄
丄 ,
, 丄
丄 ,
, ,
, ,
, .
. 丄
丄 的正弦值;
的正弦值; 外接球的体积.
外接球的体积.
 中,平面
中,平面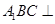 侧面
侧面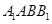 ,且
,且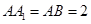
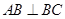 ;
;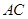 与平面
与平面 所成的角为
所成的角为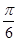 ,求锐二面角
,求锐二面角 的大小。
的大小。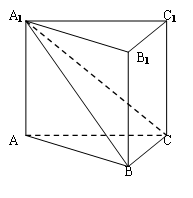
 CD=1,PD=
CD=1,PD= .
.
 ?
?

 .
. 平面
平面 .
.
 中,
中, .有下列条件:
.有下列条件: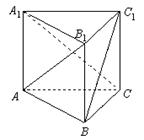
 ;②
;② ;③
;③ .其中能成为
.其中能成为 的充要条件的是(填上该条件的序号)________。
的充要条件的是(填上该条件的序号)________。