题目内容
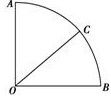
如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC和∠BOC都不小于30°的概率.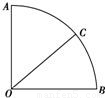
【答案】分析:本题利用几何概型求解.只须求出满足:使得∠AOC和∠BOC都不小于30°的圆心角,再将求得的角度值与整个扇形的角度求比值即得.
解答:解:将圆心角为90°的扇形等分成三部分:
当射线OC位于中间一部分时,使得∠AOC和∠BOC都不小于30°,
∴使得∠AOC和∠BOC都不小于30°的概率为:
P=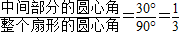 ,
,
故使得∠AOC和∠BOC都不小于30°的概率为: .
.
点评:本小题主要考查几何概型、几何概型的计算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
解答:解:将圆心角为90°的扇形等分成三部分:
当射线OC位于中间一部分时,使得∠AOC和∠BOC都不小于30°,
∴使得∠AOC和∠BOC都不小于30°的概率为:
P=
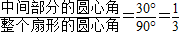 ,
,故使得∠AOC和∠BOC都不小于30°的概率为:
 .
.点评:本小题主要考查几何概型、几何概型的计算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
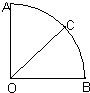 如图,在圆心角为90°的扇形中以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不小于30°的概率是( )
如图,在圆心角为90°的扇形中以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不小于30°的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC和∠BOC都不小于30°的概率.
如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC和∠BOC都不小于30°的概率.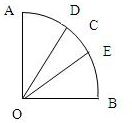 如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC 和∠BOC都不小于30°的概率
如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC 和∠BOC都不小于30°的概率
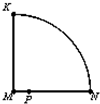 如图,在圆心角为90°的扇形MNK中,动点P从点M出发,沿MN→
如图,在圆心角为90°的扇形MNK中,动点P从点M出发,沿MN→