题目内容
如图20,AD、CF是△ABC的两条高,EF⊥AC于E点,交CB的延长线于G点,交AD于H点.求证:EF2=EH·EG.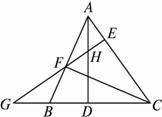
图20
思路分析:由已知条件可以得到EF2=AE·CE;由未知寻需知,即由所求证得结论,只要再证明EH·EG =AE·CE即可,而这由△AEH∽△GEC即可推出.
证明:∵CF⊥AB,EF⊥AC,∴EF2=AE·CE.?
又由AD⊥BC,可知∠AEH =∠CEG =90°,∠AHE =∠GCE,?
∴△AEH∽△GEC.∴![]() =
=![]() .?
.?
∴EH·EG =AE·CE.?
∴EF2=EH·EG.

练习册系列答案
相关题目
 (浙江卷文20)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,
(浙江卷文20)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,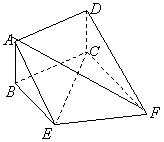 (浙江卷文20)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,
(浙江卷文20)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,