题目内容
如图,梯形ABCD中,AB=BC=1,AD=2,∠CBA=∠BAD=90°,沿对角线AC将△ABC折起,使点B在平面ACD内的射影O恰在AC上,
(Ⅰ)求证:AB⊥平面BCD;
(Ⅱ)求异面直线BC与AD所成的角;
(Ⅲ)求二面角B-AD-C的余弦值。
(Ⅰ)求证:AB⊥平面BCD;
(Ⅱ)求异面直线BC与AD所成的角;
(Ⅲ)求二面角B-AD-C的余弦值。

解:(Ⅰ)在梯形ABCD 中, ,
,
∴ ,
,
∴ ,
,
又 ,
,
∴BO⊥AC,
又AB=CB,
∴O为AC中点,
以O为坐标原点,以OA,OB所在直线分别为x,z轴,以过O且平行于CD的直线为y轴建立空间直角坐标系,
则 ,
,
∴ ,
,
∴AB⊥CD,
又AB⊥BC,
∴AB⊥平面BCD。
(Ⅱ) ,
,
∴ ,
,
∴ ,
,
即异面直线BC与AD所成的角为60°。
(Ⅲ)平面ACD的法向量为 ,设平面ABD的法向量为
,设平面ABD的法向量为 ,
,
则 ,
,
解得 ,
,
取z=1,
∴ ,
,
设二面角B-AD-C的平面角为θ,
则 。
。

练习册系列答案
相关题目
 如图,梯形ABCD中,CD∥AB,AD=DC=CB=
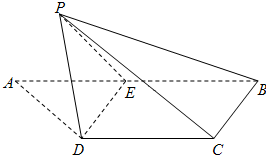
如图,梯形ABCD中,CD∥AB,AD=DC=CB= 如图,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中点,AB=BC=1,PA=AD=2.
如图,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中点,AB=BC=1,PA=AD=2. 如图,梯形ABCD中,CD∥AB,
如图,梯形ABCD中,CD∥AB,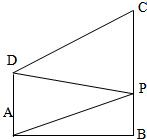 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是BC上的动点,当
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是BC上的动点,当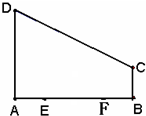 如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.
如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.