Question

如图所示，在排成4×4方阵的16个点中，中心位置4个点在某圆内，其余12个点在圆外.从16个点中任选3点，作为三角形的顶点，其中至少有一个顶点在圆内的三角形共有多少个？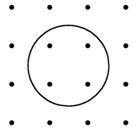

Answer 1

错解1：16个点中任取3个有种方法，其中三个点都不在圆内的有种，故满足题设条件的三角形有-=340个.

错解2：要作出符合题意的三角形，从圆内四点中：

①任取3点，有种；

②任取2点，圆外取1点，有种；

③任取1点，圆外取2点，有种.

综上可知，至少有一个顶点在圆内的三角形共有++=340个.

剖析：错解1中不符合题意的还有两种情形：一是4点共线，但其中任意3点至少有1点在圆内，这样的4点有6种；还有就是只有3点共线，但其中恰有1点在圆内，这样的3点有4种.因此，正确解法是：--6-4=312种.

错解2错在②③两种情形，其中所取的3点可能是共线的.因此，要兼顾题中的两个约束条件：所取三点可作成三角形；至少有一个点在圆内.因此正确解法是：从圆内四点中任取.

①3点，有种；

②2点，圆外12点中取1点，有种；

③1点，圆外12点中取2点，有（-4）种.

综上可知，所求的三角形共有++（-4）=312个.