题目内容
与直线 和圆
和圆 都相切的半径最小的圆的方程是( )
都相切的半径最小的圆的方程是( )
A. | B. |
C. | D. |
C
解析试题分析:由题意先确定圆心的位置,再结合选项进行排除,并得到圆心坐标,再求出所求圆的半径.
考点:直线与圆的关系.

练习册系列答案
相关题目
已知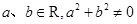 ,则直线
,则直线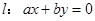 与圆:
与圆: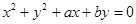 的位置关系是( ).
的位置关系是( ).
| A.相交 | B.相切 | C.相离 | D.不能确定 |
圆 关于直线
关于直线 对称的圆的方程为( )
对称的圆的方程为( )
A. | B. |
C. | D. |
动圆C经过点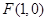 ,并且与直线
,并且与直线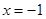 相切,若动圆C与直线
相切,若动圆C与直线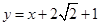 总有公共点,则圆C的面积( )
总有公共点,则圆C的面积( )
A.有最大值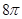 | B.有最小值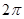 | C.有最小值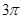 | D.有最小值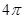 |
圆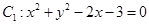 与圆
与圆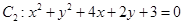 的位置关系为 ( )
的位置关系为 ( )
| A.两圆相交 | B.两圆相外切 | C.两圆相内切 | D.两圆相离 |
若直线2x-y+a=0与圆(x-1)2+y2=1有公共点,则实数a的取值范围是( )
A.-2-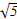 <a<-2+ <a<-2+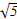 |
B.-2-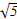 ≤a≤-2+ ≤a≤-2+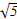 |
C.-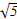 ≤a≤ ≤a≤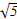 |
D.-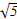 <a< <a<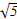 |
设过点(0,b)且斜率为1的直线与圆x2+y2+2x=0相切,则b的值为( )
A.2± | B.2±2 | C.1± | D. ±1 ±1 |
若直线ax+2by-2=0(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则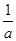 +
+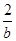 的最小值为( )
的最小值为( )
| A.1 | B.5 | C.3+4 | D.3+2 |
若直线过点P 且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).
且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).
| A.3x+4y+15=0 | B.x=-3或y=-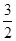 |
| C.x=-3 | D.x=-3或3x+4y+15=0 |