题目内容
已知数列{an}满足an>0,a1=m,其中0<m<1,函数 .
.
(1)若数列{an}满足an+1=f(an),(n≥1,n∈N),求an;
(2)若数列{an}满足an+1≤f(an),(n≥1,n∈N).数列{bn}满足 ,求证:b1+b2+…+bn<1.
,求证:b1+b2+…+bn<1.
解:(1)由题设知 ,
,
∴ .
.
∴
∴ 是以
是以 为首项1为差的等差数列,
为首项1为差的等差数列,
∴
∴
(2)由条件可得: .
.
∴
∴
∴
∴

∵0<m<1
∴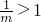
∴
∴
∴ .
.
分析:(1)由 ,知
,知 .所以
.所以 ,由此能求出an.(2)由
,由此能求出an.(2)由 .知
.知 ,所以
,所以 .由此能够证明b1+b2+…+bn<1.
.由此能够证明b1+b2+…+bn<1.
点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,注意递推公式的灵活运用.
 ,
,∴
 .
.∴

∴
 是以
是以 为首项1为差的等差数列,
为首项1为差的等差数列,∴

∴

(2)由条件可得:
 .
.∴

∴

∴

∴


∵0<m<1
∴
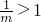
∴

∴

∴
 .
.分析:(1)由
 ,知
,知 .所以
.所以 ,由此能求出an.(2)由
,由此能求出an.(2)由 .知
.知 ,所以
,所以 .由此能够证明b1+b2+…+bn<1.
.由此能够证明b1+b2+…+bn<1.点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,注意递推公式的灵活运用.

练习册系列答案
相关题目