题目内容
函数f（x）=2x2-lnx在其定义域的一个子区间（k-1，k+1）内部是单调函数，则实数k的取值范围是
- A.
- B.
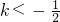
- C.
＜
- D.
A
分析：对函数求导，分别令导数大于0，小于0，得x的取值范围，即可得f（x）的单调性，结合函数f（x）的图象得出k满足的不等式，进而可求出k的取值范围．
解答：f′（x）=4x-
=
，
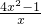令f′（x）＞0，得x＞
，令f′（x）＜0，得0＜x＜，
∴函数f（x）在（0，]上是减函数，在[，+∞）上是增函数，
∵函数f（x）在其定义域的一个子区间（k-1，k+1）上是单调函数，
∵区间（k-1，k+1）的长度为2，∴只能k-1
，解得k
故选A．
点评：本题考查利用导数研究函数的单调性，属基础题．
分析：对函数求导，分别令导数大于0，小于0，得x的取值范围，即可得f（x）的单调性，结合函数f（x）的图象得出k满足的不等式，进而可求出k的取值范围．
解答：f′（x）=4x-
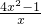=，令f′（x）＞0，得x＞
，令f′（x）＜0，得0＜x＜，∴函数f（x）在（0，
]上是减函数，在[，+∞）上是增函数，∵函数f（x）在其定义域的一个子区间（k-1，k+1）上是单调函数，
∵区间（k-1，k+1）的长度为2，∴只能k-1
，解得k故选A．
点评：本题考查利用导数研究函数的单调性，属基础题．
练习册系列答案
相关题目
函数f（x）=2x2-6x+1在区间[-1，1]上的最小值为（ ）
| A、9 | ||
| B、-3 | ||
C、
| ||
D、
|