题目内容
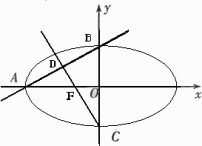
如图,椭圆![]() (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).

(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
答案:
解析:
解析:
|
解法一: (Ⅰ)由题设a=2,c=1,从而b2=a2-c2=3, 所以椭圆C前方程为 (Ⅱ)(i)由题意得F(1,0),N(4,0). 设A(m,n),则B(m,-n)(n≠0), AF与BN的方程分别为:n(x-1)-(m-1)y=0, n(x-4)-(m-4)y=0. 设M(x0,y0),则有 由②,③得 x0=
所以点M恒在椭圆G上. (ⅱ)设AM的方程为x=xy+1,代入 设A(x1,y1),M(x2,y2),则有:y1+y2= |y1-y2|= 令3t2+4=λ(λ≥4),则 |y1-y2|= 因为λ≥4,0< |y1-y2|有最大值3,此时AM过点F. △AMN的面积S△AMN= 解法二: (Ⅰ)问解法一: (Ⅱ)(ⅰ)由题意得F(1,0),N(4,0). 设A(m,n),则B(m,-n)(n≠0), AF与BN的方程分别为:n(x-1)-(m-1)y=0, ② n(x-4)-(m-4)y=0, ③ 由②,③得:当≠ 由④代入①,得 当x= 解得 所以点M的轨迹方程为 (Ⅱ)同解法一. 本小题主要考查直线与椭圆的位置关系、轨迹方程、不等式等基本知识,考查运算能力和综合解题能力,满分14分. |

练习册系列答案
相关题目






 (a>b>0)的上、下两个顶点为A、B,直线l:
(a>b>0)的上、下两个顶点为A、B,直线l: ,点P是椭圆上异于点A、B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为
,点P是椭圆上异于点A、B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为 ,BP所在的直线的斜率为
,BP所在的直线的斜率为 .若椭圆的离心率为
.若椭圆的离心率为 ,且过点
,且过点 .
. 的值;
的值; (a>b>0)的上、下顶点分别为A、B,已知点B在直线l:y=-1上,且椭圆的离心率e =
(a>b>0)的上、下顶点分别为A、B,已知点B在直线l:y=-1上,且椭圆的离心率e = .(Ⅰ)求椭圆的标准方程;
.(Ⅰ)求椭圆的标准方程;