题目内容
求下列函数的值域:
(1)函数y=x2+4x-2,x∈R的值域为______;
(2)函数y=x-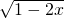 的值域为______;
的值域为______;
(3)已知x∈R,且x≠0,则函数y=x2+ -x-
-x- 的值域为______;
的值域为______;
(4)函数y= 的值域为______.
的值域为______.
(5)函数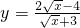 的值域为______.
的值域为______.
解:(1)配方法:由于y=x2+4x-2=(x+2)2-6,则y≥-6,故其值域为[-6,+∞);
(2)换元法:令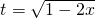 (t≥0),则y=x-
(t≥0),则y=x-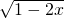 =
=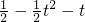 =
=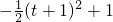 (t≥0),
(t≥0),
故y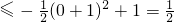 ,故其值域为
,故其值域为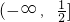 ;
;
(3)换元法:令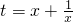 (t≥2),则函数y=x2+
(t≥2),则函数y=x2+ -x-
-x- =
=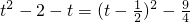 ,
,
由于t≥2,则y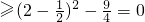 ,故其值域为[0,+∞);
,故其值域为[0,+∞);
(4)分离常数法:y= =
=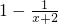 ,由于x+2≠0,则y≠1,故其值域为(-∞,1)∪(1,+∞);
,由于x+2≠0,则y≠1,故其值域为(-∞,1)∪(1,+∞);
(5)分离常数法: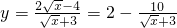 ,
,
由于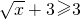 ,∴
,∴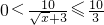 ,则
,则 ,即
,即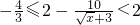 ,故其值域为
,故其值域为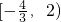 .
.
分析:(1)配方法:首先把原函数配方变为(x+2)2-6,则值域可求;
(2)换元法:令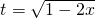 ,则利于二次函数在闭区间上的最值得到值域;
,则利于二次函数在闭区间上的最值得到值域;
(3)换元法:令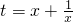 ,同(2)类似得到;
,同(2)类似得到;
(4)分离常数法:y= =
=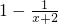 ,则值域可求;
,则值域可求;
(5)分离常数法: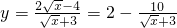 则值域可求.
则值域可求.
点评:本题考查了函数值域的求法,考查了配方法,换元法,分离常数法等,考生要重点掌握.
(2)换元法:令
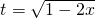 (t≥0),则y=x-
(t≥0),则y=x-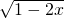 =
=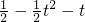 =
=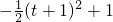 (t≥0),
(t≥0),故y
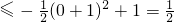 ,故其值域为
,故其值域为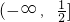 ;
;(3)换元法:令
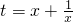 (t≥2),则函数y=x2+
(t≥2),则函数y=x2+ -x-
-x- =
=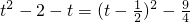 ,
,由于t≥2,则y
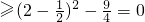 ,故其值域为[0,+∞);
,故其值域为[0,+∞);(4)分离常数法:y=
 =
=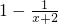 ,由于x+2≠0,则y≠1,故其值域为(-∞,1)∪(1,+∞);
,由于x+2≠0,则y≠1,故其值域为(-∞,1)∪(1,+∞);(5)分离常数法:
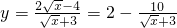 ,
,由于
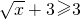 ,∴
,∴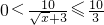 ,则
,则 ,即
,即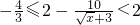 ,故其值域为
,故其值域为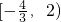 .
.分析:(1)配方法:首先把原函数配方变为(x+2)2-6,则值域可求;
(2)换元法:令
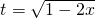 ,则利于二次函数在闭区间上的最值得到值域;
,则利于二次函数在闭区间上的最值得到值域;(3)换元法:令
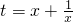 ,同(2)类似得到;
,同(2)类似得到;(4)分离常数法:y=
 =
=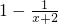 ,则值域可求;
,则值域可求;(5)分离常数法:
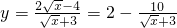 则值域可求.
则值域可求.点评:本题考查了函数值域的求法,考查了配方法,换元法,分离常数法等,考生要重点掌握.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目