题目内容
已知数列{an}满足an2=an-1an+1(n∈N*,n≥2),若 ,a4a6=4,则a4+a5+a6=________.
,a4a6=4,则a4+a5+a6=________.
4
分析:由已知an2=an-1an+1得到a52=a4a6,再由a4a6=4,即可求出a5的值,然后把已知的 中等号左边的一三项结合通分后,把a4a6=4和a5的值代入即可求出a4+a6的和,把a4+a6的和与a5的值代入所求的式子中即可求出值.
中等号左边的一三项结合通分后,把a4a6=4和a5的值代入即可求出a4+a6的和,把a4+a6的和与a5的值代入所求的式子中即可求出值.
解答:由an2=an-1an+1得到a52=a4a6=4,解得a5=±2,
当a5=2时,由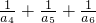 =
= =
=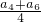 +
+ =1,解得a4+a6=2,所以a4+a5+a6=2+2=4;
=1,解得a4+a6=2,所以a4+a5+a6=2+2=4;
当a5=-2时,由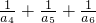 =
= =
=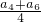 -
- =1,解得a4+a6=6,所以a4+a5+a6=6-2=4.
=1,解得a4+a6=6,所以a4+a5+a6=6-2=4.
综上,a4+a5+a6=4.
故答案为:4
点评:此题考查学生灵活运用等比数列的性质化简求值,是一道中档题.
分析:由已知an2=an-1an+1得到a52=a4a6,再由a4a6=4,即可求出a5的值,然后把已知的
 中等号左边的一三项结合通分后,把a4a6=4和a5的值代入即可求出a4+a6的和,把a4+a6的和与a5的值代入所求的式子中即可求出值.
中等号左边的一三项结合通分后,把a4a6=4和a5的值代入即可求出a4+a6的和,把a4+a6的和与a5的值代入所求的式子中即可求出值.解答:由an2=an-1an+1得到a52=a4a6=4,解得a5=±2,
当a5=2时,由
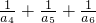 =
= =
=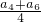 +
+ =1,解得a4+a6=2,所以a4+a5+a6=2+2=4;
=1,解得a4+a6=2,所以a4+a5+a6=2+2=4;当a5=-2时,由
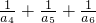 =
= =
=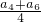 -
- =1,解得a4+a6=6,所以a4+a5+a6=6-2=4.
=1,解得a4+a6=6,所以a4+a5+a6=6-2=4.综上,a4+a5+a6=4.
故答案为:4
点评:此题考查学生灵活运用等比数列的性质化简求值,是一道中档题.

练习册系列答案
相关题目