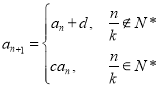题目内容
【题目】某校抽取了100名学生期中考试的英语和数学成绩，已知成绩都不低于100分，其中英语成绩的频率分布直方图如图所示，成绩分组区间是
，
，
，
，
.
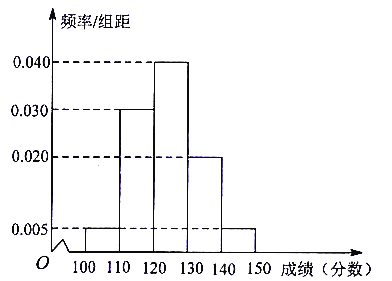
（1）根据频率分布直方图，估计这100名学生英语成绩的平均数和中位数（同一组数据用该区间的中点值作代表）；
（2）若这100名学生数学成绩分数段的人数y的情况如下表所示：
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间内英语人数与数学人数之比为
，现从数学成绩在
的学生中随机选取2人，求选出的2人中恰好有1人数学成绩在的概率.
【答案】（1）这100名学生英语成绩的平均数和中位数分别为
，
（2）
【解析】
（1）利用频率分布直方图求平均数，中位数的方法求解即可；
（2）利用题设条件得出
的值，再由古典概型的概率公式求解即可.
（1）这100名学生英语成绩的平均数为
设这100名学生英语成绩的中位数为
直方图可知
对应的频率分别为
，解得
则这100名学生英语成绩的中位数为
（2）区间
内英语人数为
人
区间内数学人数为
人
设数学成绩在的人记为
，数学成绩在
的人记为
则从数学成绩在
的学生中随机选取2人的所有情况为
，
，
，共10种，其中选出的2人中恰好有1人数学成绩在有6种
即选出的2人中恰好有1人数学成绩在的概率为
练习册系列答案
阅读快车系列答案
相关题目
